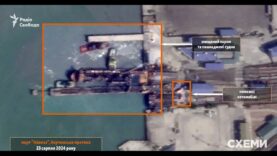
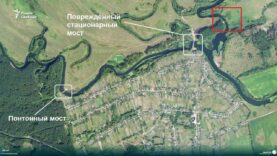
Kursk: Russian Friendly Fire on BMP, Pontoon and Zvannoe Bridge Hit Again, Two Howitzers Destroyed
Video Summary
The concept of prime numbers has fascinated mathematicians for centuries, and their unique properties have garnered significant attention in modern cryptography. Primality testing is crucial in determining whether a given number is prime or composite. Researchers have developed various algorithms to test for primality, with the most efficient being the AKS primality test.
However, this test is not suitable for large numbers due to its high computational complexity. A more recent development is the Pollard’s rho algorithm, which is simpler and more efficient, but it is not deterministic, meaning it may not always return the correct result. Another approach is the Baillie-PSW primality test, which is more complex and computational intensive but has been shown to be reliable.
Primality testing has practical applications in computer science, such as public-key cryptography, where large prime numbers are used to secure online transactions and communication. Developing faster and more efficient primality tests is crucial for advancing the field of cryptography and ensuring the security of online transactions.
Related posts:
Putin’s Crypto Scheme to Beat Sanctions Is Failing!
Ukraine state-owned enterprises weekly — Issue 152
Heavily Sanctioned Russia Resorts to BARTER SYSTEM to Pay for Chinese Goods!
The Secrets of Sary Shagan – The Strange Yet Important Site
Kursk: Russia Builds Pontoon Bridge Near Destroyed Glushkovo Bridge, Ka-52 Crash Site, T-72 Captured
Ukrainian BMP-2 Destroys Russian BMP-2 from 400 Meters Near Vuhledar: Russian BMP Then Captured!
Kursk: HIMARS Destroys a Pontoon, Russian Friendly Fire on Column in Korenevo, T-90M Captured
Time names Ukraine's online wedding service among best inventions of 2024
